讓考生抱鴨蛋的幾何試題

有趣的考題

昨晚April 19 2013  一家上 遠企 小吃，看到超市賣日本進口的 "熟食玉米", 一支 標價 128元。
今天菜市場回來，正在啃兩支 50元的玉米，一樣是蒸熟的，只是沒有真空包裝而已。

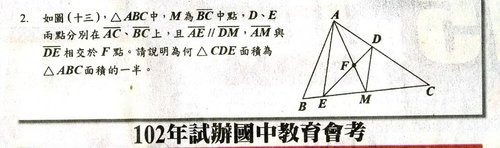
啃到一半，老妻給我報紙上的試題，說她很喜愛 幾何，但是一時解不出來。

我拿一張小紙條，劃幾下，還沒啃完玉米棒，就交捲了。

您要操腦一下嗎？
提示：三角形面積是  底乘高除2

我初中畢業簽名簿上有一頁是學長給的幾何證明。

今天得到同學的回應如下：

Rubie Chen <rubiechen@sympatico.ca> 於 2013年4月20日下午12:06 寫道：

我也可得滿分！

AMC = 0.5 ABC

AFD = EMF

把 AFD 翻下來填補 EMF

所以 CDE = 0.5 ABC

----- Original Message -----

From: NanLoh Yang-cepm   Saturday, April 20, 2013 6:31 PM

Subject: RE: 讓考生抱鴨蛋的幾何試題

Sear Stein:

I am submitting my home work assignment for your consideration:

Since E is only defined as on  line-BC, with your permission I am placing it 2 nm away from point B((or smack on top of B. Then MD //AB(E).

∆  AB(E)C and∆CDE(B)  share the same  angle   ѵDEM with 2 corresponding sides at half the lemgth, ie. CD=1/2 CA and CM=1/2 CB(E).  QED (I think)

  I hope this submision meets with your approval. If so, I demand a teacher's reward of a cup of top quality coffee during my next Taipei visit .

 Nan Loh

2013/4/21 Rubie Chen <rubiechen@sympatico.ca>

Hi, Nan Loh： 

 

你的解答不被Rubie接受. 因為：

1. Pt.E has been defined not only a point on line-BC， but it also has been so placed that AE must be parallel to DM (i.e., AE//DM). 
2. Pt.B and Pt.E must always be two separated points.

Respect the above conditions and think it over again.

 

Best wishes

Rubie

我回他

Nan Loh：
Sorry, not yet QED = quod erat demonstrandum 【拉】

unfortunately 證明未了


認真閱卷，是比交卷的考生要辛苦幾倍。

Nan Loh兄當然可以把E點定位在靠近B點 nm，證明這個特例成立。
但是其他E點定位還是沒有證明出來。

因此 您只能贏得一杯 台北咖啡店通常會賣的 "美式咖啡"，就是那一種淡而無味，我在貴寶地大賣場Mall喝 到的免費咖啡.。

這個命題裡，D, E兩點的定位，只有一個Freedom "自由度"。

請參見下面附件 我加註的原圖。

把D點沿AC線向A點移到A-nm時，E點只好移到M-nm 才能維持 AE//DM,
反之，
把D點沿AC線向C點，E點只好移到B-nm 為限，不能超過線外。這時候要維持 AE//DM, D點就限制到G-nm點。
這就是您的特例。

 
stein上




今天 April 22得到 Nan Loh 要求補考
我回他：


Hi, Nan Loh:

還是要感謝您跟Rubie的參與，讓這個幾何題變得很有趣。

Rubie提醒過 您題目沒有看清楚，我也說 您舉的特例，把E點移到B點，讓D點定位在AC中點，

特例是成立了，但是並不能證明通例就可以成立。

幾何證明需要嚴謹的推論。這也是引人入勝的地方。

我要是考生的話，會回答：

三角形面積是底乘高除2。
因為AE//DM，因此ADM 跟 EDM共用DE底線的兩個3角形，他們的高度是相等的，
因此他們的面積是相等的。

這兩個3角形分別加上3角形DMC之後，得到的兩個3角形AMC 跟EDC面積也是相等的。

因為M是 BC中點，故三角形AMC是 3角形ABC的一半，

由此可證
3角形CDE等於三角形AMC，等於 3角形ABC的一半。

Q.E.D.


我要引用您的話：
If so, I demand a teacher's reward of a cup of top quality coffee during your next Taipei visit .

但是不再從寬解釋 teacher's reward 是老師的"打賞"，而是要從嚴解釋 teacher's reward 是老師的"酬勞".

我初中的幾何老師，下課之前，會在黑板上出幾個題目， 點名同學上台，然後過一會兒，就會帶著凌辱一般的笑容說：
證明不出來，也不要緊了，書不用唸，去街頭擺攤賣包子， 賺錢多多喔。
大家背後叫他”包阿”（台語 肉包子的發音）。

說的也是，看看鼎泰豐多賺錢，幾何再好，頂多是當 美國律師，賺錢還是差多了。

祝好