THORENS TD 295 LP player 調整

我這台Thorens唱盤配幾樣唱頭， Shure V15, Grado Silver, Gold, Denon DL 160, DL 103安裝時候完全按照說明書，配合隨機附送的Guage 治具（下圖 1,2, 3）沒甚麼問題。
自從2年前Colin 網站提起，要沿著唱針從外到內，調出兩個正切點A and B. 有人給我analog雜誌附的調整卡紙，我買AT唱盤，LP-Gears也附上一張單點卡紙，好像非此不可。
上週初闖Myav，也有熱心網友強烈建議要自己畫圖，核對，不能目測了事。



我現在找出來Thorens 說明書再讀一遍，實機核對。




先要核對下圖 figure A 的唱針身高：
這相當於Vertical Tracking Angle (VTA)
高度不夠要加隨機附送的墊片。
萬一太高的話，這機子恐怕沒辦法矯正。
否則高度太低，唱針跑起來"頭犁犁"，高度太高，跑起來昂首闊步，不合原設計。
道理是說唱溝刻刀下的時候是跟盤面垂直的，重播的唱針當然也要跟著垂直才對。後來某國高人發現，刻出來的溝槽會縮水，未必垂直。
金耳朵聽出來身高差個 1 mm聲音高低頻有差。
還有拿顯微鏡檢視調整垂直度VTA的。
不妨計算一下：
半徑250mm (9吋唱臂）的圓圈，周長等於＝2*3.1416*250=1570mm涵蓋360度，或者說：
上下 1 mm=0.23度，
1度＝4.4 mm
角度的變化其實不大呢。
12吋的長臂更小。


effective length有效臂長是指支點到針頭的距離，規格上寫232 mm。
實際上要精確測量不容易。
我拿直尺量到唱頭前端=234 mm再扣除唱針到前端的 2mm（查DL 160規格）得到232 mm。這是唱頭遵照治具調出來的。
stylus overhang唱針超距規格上寫16.4mm. 實機沒法測量，因為唱臂無法移動到唱片軸心上頭比劃。
軸心到支點的距離有人稱作mounting distance。實機測離約 207 mm。
按照定義：mounting distance + overhang = effective length
可是 207 + 16 = 223 mm 差規格的232 mm 有 9 mm之多，絕非老花眼可以解釋。
以老人之心度小人之腹，可能Thorens技術頭原來建議客戶設定overhang=16.4 mm，加上mounting distance 207 mm就老實寫上232mm，銷售經理一看，effective length越長越好，輸人不輸陣，大筆一揮，反勾一下，223搖身一變232mm, 還說將來有龜毛Stein問起的話，有我來檔。
這是開玩笑的了。
Thorens說明書 德文寫Ueberhang(einstellbar) 16.4 mm 可以調整，並非固定之意。
事實上唱頭固定螺絲溝槽長 10 mm，可以進退+/-3 mm。要是推到最前端，effective length 會到232 mm沒錯。


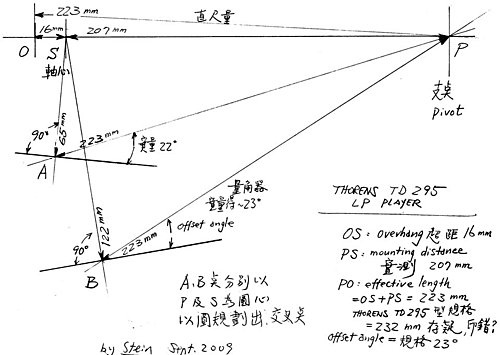
offset angle=23度，我借用半圓塑膠角度規，量一下治具的邊緣，證實沒錯。






按照治具調出來，量到mounting distance =207 mm, effective length =223 mm.
我在白紙上劃兩個三角形
207/223/65 mm相當A點
207/223/122 mm相當B點
用半圓塑膠角度規，量一下A,B點的offset angles，跟23度出入不大，在我畫圖的誤差之內。










以前1974年用的GA212也提供治具，換裝唱頭更加簡單。








Mr. Seb已經畫圖，提出一個名稱叫linear offset相當下圖裡的

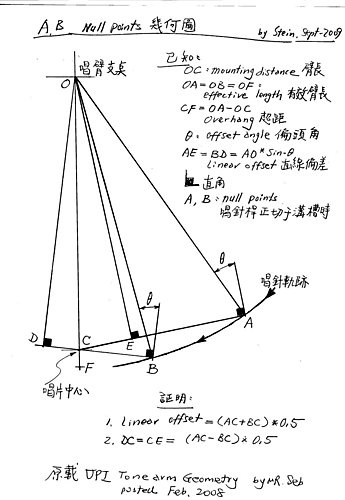
DB and AE. (Linear offset = NP1+DC, or  = NP2-CE)

證明過

linear offset is (NP1+NP2) / 2
And
DC = CE = (NP2-NP1) / 2

只要您訂出來溝槽跟唱針直切的A,B點，知道NP1, NP2要多少，就可以算計出來相當的offset angle, 按照關係'三角函數表就可以找出來：

effective length * sin (offset angle)= linear offset.

而overhang
從：OE=effective lenght * cos(offset angle),  跟直角三角形E─C─O算出mounting distance OC

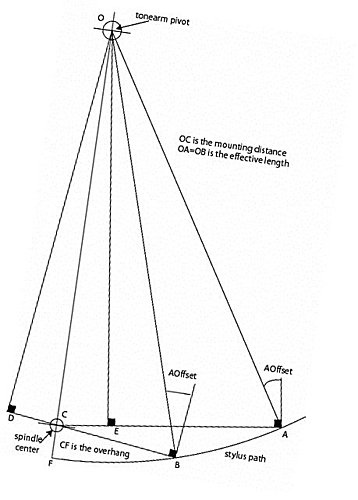
Null points are measured by their distance to the spindle centre i.e. AC (NP2) and CB (NP1). The angle formed by the line passing through the stylus and the pivot of the tonearm and the projection of the cantilever onto the record's surface is named the offset angle (AOffset). Once set up, the offset angle is fixed. 

Linear offset.

The linear offset is given by OA* Sin (offset angle) = OB* Sin (offset angle) (since OA and OB are equal to the effective length).

This linear offset is equal to DB and AE.  Therefore, it follows that:
Linear offset = NP1+DC
Linear offset = NP2-CE

Let's now take a look at the triangles ODC and OEC with right angles at D and E. Those triangles share one common side, OC. and OD = OE = OA * Cos (offset angle) = OB * Cos (offset angle). It follows that DC=CE

And then the linear offset is (NP1+NP2) / 2
And
DC = CE = (NP2-NP1) / 2

Whatever the effective length, if you choose a pair a null points, the linear offset is simply a function of the pair of null points you choose.

I asked VPI jig users to measure the angle OCB on their jig. What is the theoretical value of this angle?

Let's begin with the DCO angle – once we have this angle, OCB will be 180-DCO.

DCO is given by: ArcCos ((NP2-NP1) / (2OC))
And then, OCB is 180 - ArcCos ((NP2-NP1) / (2OC))

Remember that OC is the mounting distance and for a given pair of null points, the angle OCB is a function of the mounting distance.

Let's call the angle measured by users, Alpha.

Our goal here is to obtain the value of the second null point (since it's not provided by VPI). Let's consider the mounting distance as known. We now need to resolve this equation:

Alpha = 180 – ArcCos ((NP2-NP1) / (2OC))

180 – Alpha = ArcCos ((NP2-NP1) / (2OC))

Cos (180 – Alpha) = ((NP2-NP1) / (2OC))

NP2 = 2OC * Cos (180 – Alpha) + NP1

Once we know the second null point, all other data relating to the geometry of the tonearm alignment can be calculated from the following equations:

Effective length = (OC² +NP1*NP2)^0.5

Angular offset = ArcSin ((NP1+NP2) / (2*Effective length))